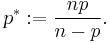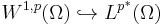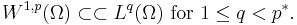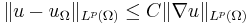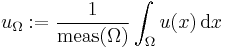Rellich–Kondrachov theorem

In mathematics, the Rellich-Kondrachov theorem is a compact embedding theorem concerning Sobolev spaces. It is named after the Italian-Austrian mathematician Franz Rellich and the Russian mathematician Vladimir Iosifovich Kondrashov.

Statement of the theorem

Let Ω ⊆ Rn be an open, bounded Lipschitz domain, and let 1 ≤ p < n. Set

p^{*}�:= \frac{n p}{n - p}.

Then the Sobolev space W1,p(Ω; R) is continuously embedded in the Lp space Lp∗(Ω; R) and is compactly embedded in Lq(Ω; R) for every 1 ≤ q < p∗. In symbols,

W^{1, p} (\Omega) \hookrightarrow L^{p^{*}} (\Omega)

and

W^{1, p} (\Omega) \subset \subset L^{q} (\Omega) \mbox{ for } 1 \leq q < p^{*}.

Consequences

Since an embedding is compact if and only if the inclusion (identity) operator is a compact operator, the Rellich-Kondrachov theorem implies that any uniformly bounded sequence in W1,p(Ω; R) has a subsequence that converges in Lq(Ω; R). Stated in this form, the result is sometimes known as the Rellich-Kondrachov selection theorem (since one "selects" a convergent subsequence).

The Rellich-Kondrachov theorem may be used to prove the Poincaré inequality, which states that for u ∈ W1,p(Ω; R) (where Ω satisfies the same hypotheses as above),

\| u - u_{\Omega} \|_{L^{p} (\Omega)} \leq C \| \nabla u \|_{L^{p} (\Omega)}

for some constant C depending only on p and the geometry of the domain Ω, where

u_{\Omega}�:= \frac{1}{\mathrm{meas} (\Omega)} \int_{\Omega} u(x) \, \mathrm{d} x

denotes the mean value of u over Ω.

References